Online Notes for Diploma in IT/ICT Course: Binary Fractions

So far we have only looked at whole numbers (integers), we need to understand how computer represent fractions.

You should have learnt at Primary School how a denary fraction works:

10	1		$\frac {1}{10}$	$\frac {1}{100}$
$10^1$	$10^0$		$10^{-1}$	$10^{-2}$
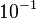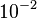1	2	.	7	5

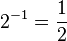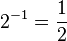As you can see, the column headings have been extended to $10^{-1}=\frac {1}{10}$ and $10^{-2}=\frac {1}{100}$ . We can do the same thing in binary with the column headings $2^{-1}=\frac {1}{2}$ , $2^{-2}=\frac {1}{4}$ , and so on. The number 12.75 in 8 bit binary with 4 bits after the decimal point is therefore 8 + 4 + 0.5 + 0.25:

8	4	2	1		$\frac {1}{2}$	$\frac {1}{4}$	$\frac {1}{8}$	$\frac {1}{16}$
$2^3$	$2^2$	$2^1$	$2^0$		$2^{-1}$	$2^{-2}$	$2^{-3}$	$2^{-4}$
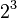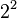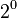1	1	0	0	.	1	1	0	0

Notice that for the same number of bits after the point, the binary fraction is less accurate. It can only take 4 different values, whereas the denary number can have 100 different divisions with two digits. You'll see in a moment how this can be troublesome.

Converting Binary to Decimal

We are going to convert the number 6.125 into a binary decimal by using the grid below

8	4	2	1		$\frac {1}{2}$	$\frac {1}{4}$	$\frac {1}{8}$	$\frac {1}{16}$
0	1	1	0	.	0	0	1	0

This seems simple enough as 6.125 = 4 + 2 + 0.125, but what about this more interesting number: 6.4

8	4	2	1		$\frac {1}{2}$	$\frac {1}{4}$	$\frac {1}{8}$	$\frac {1}{16}$
0	1	1	0	.	0	1	1	0

But this doesn't look right?! This number isn't correct as it only reaches 4 + 2 + 0.25 + 0.125 = 6.375, we need some more bits for the decimal places. However, in a computer you might be restricted to the number of bits you can use, so we'll use the number closest to the one we were aiming for. You feel a bit annoyed at this, but don't worry, you make this compromise every time that you try to represent $\frac {1}{3}$ in denary, or 0.33333333; you see what I mean.

converting from denary to binary fractions

Now try some questions yourself and see how you get on. Remember, where there aren't enough bits for the decimal place, write down the number closest to your target number. In each case use 8 bits for the binary with four bits after the decimal point:

7.5

Answer :

0111.1000

4.5625

Answer :

0100.1001

1.6

Answer :

0001.1001 (this is the closest we are going to get)

3.3333333

Answer :

0011.0101 (this is the closest we are going to get)

Try and convert these binary fractions into denary:

0111.0100

Answer :

7.25

1011.1001

Answer :

11.5625 (notice that we treated this as a positive number, some of you might already know about twos complement, if you haven't heard about it before, don't worry, we'll get there very soon)
To interpret it as a two's complement number let's flip it: 0100.0111 = 4 + 0.25 + 0.125 + 0.0625 = -4.4375

If I want to increase the range of numbers stored in a fixed point binary number, what should I do?

Answer

Increase the number of bits before the decimal point

If I want to increase the accuracy of numbers stored in a fixed point binary number, what should I do?

Answer :

Increase the number of bits after the decimal point

Online Notes for Diploma in IT/ICT Course

Sunday, May 19, 2013

Binary Fractions

No comments:

Post a Comment